Mathematik zum Orbit-Fraktal

Das Orbit-Fraktal ist die die grafische Darstellung der diskreten numerischen Simulation der Bahnkurve eines Objekts durch ein durch mehrere Attraktoren bzw. Kraftfeldzentren erzeugtes fiktives Kraftfeld.
Oder kürzer: die "Flugbahn" eines Objekts durch sich überlagernde Kraftfelder.

Im Fall der in den Galerien dargestellten Kurven sind um sämtliche Attraktoren Kraftfelder angeordnet (jeweils eins), deren Stärken umgekehrt proportional zur Entfernung oder zum Quadrat der Entfernung des Objektes vom jeweiligen Attraktor abnehmen und die das Objekt zu den jeweiligen Attraktoren hin beschleunigen. 
umgekehrte lineare Proportionalität:
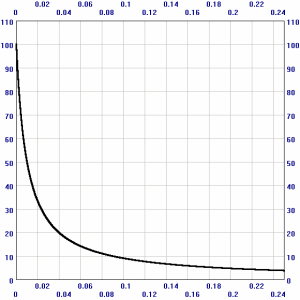
F=s/(r+eps)

umgekehrte quadratische Proportionalität:
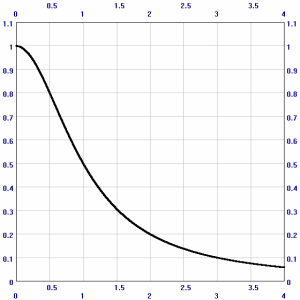
F=s/(r*r+eps)

Variablen:
   F: Beschleunigungskraft
   s: Grundwert der Feldstärke
   r: Abstand zwischen Objekt und jeweiligem Attraktor
 eps: Konstante zur Vermeidung der Division durch Null
      (Wie jedem einleuchtet gibt es auch bei natürlichen Kraftfeldern
       keine unendlich großen Feldstärken, da z.B. elektrische Ladungen
       oder Massen nie punktförmig auftreten. (Ausnahme: Singularität)
       Ansonsten müßte man für jeden Attraktor einen "Ereignishorizont"
       zur Vermeidung der Division durch Null festlegen, das gäbe aber
       den sehr sehr häßlichen Effekt, daß das Objekt bei zu großer
       Annäherung an einen Attraktor "verschluckt" würde,
       wie es durch schwarze Löcher wenig vornehm praktiziert wird)
F=1/(r+0.01) F=1/(r*r+1)

Beim einem Teil der Kurven ist die Anziehungskraft umgekehrt proportional zum Quadrat des jeweiligen Abstandes definiert, wie es der Schöpfer unseres Universums beispielsweise für die elektrische Feldstärke oder die Gravitation getan hat. Auch eine umgekehrte Proportionalität höherer Ordnung würde bestimmt hübsche Bahnkurven ergeben. Lustig wäre möglicherweise auch die Mischung mehrerer Arten von Kraftfeldern oder deren Anwendung im drei- oder höherdimensionalen Raum.
(da kann man sich leicht vorstellen, daß einem Planeten auf seinem Weg durch ein System mit mehreren Sonnen schon mal kotzübel werden kann, zumal die Sonnen sich ja auch noch bewegen...)
Übrigens arbeiten Programme zur Simulation mancher physikalischer Vorgänge recht ähnlich, z.B. Simulationen für die Bewegung von Himmelskörpern unter Einwirkung von Gravitationsfeldern oder die Bewegung elektrisch geladener Partikel in elektrischen oder magnetischen Feldern.

Zusätzlich habe ich eine Dämpfung der Bewegung eingebaut, vielleicht vergleichbar mit einem Roll-, Gleit- oder Strömungswiderstand.

Das war's eigentlich schon. Mit ein bißchen Vektorrechnung lassen sich ähnliche Programme leicht selbst entwickeln.

Übergeordnetes Verzeichnis